上一篇〈債券價格波動大解析〉介紹了債券價格的波動性質,今天把衡量價格波動的「方法」給補上,大家算是功德圓滿,對債券的價格波動有基礎的瞭解了。本篇希望可以把存續期間的概念講得淺顯易懂,但又不失深度!比較艱澀的數學推導,會放在文章的最末段,免得影響閱讀。
之前小黑也有寫過一篇〈債券的存續期間是什麼〉,本篇會更延伸與深入一些,大家不妨先複習一下。
衡量債券價格波動的方法有三種:(以下變動量都以△表示,變化率會標註%)
(1) PVBP基點價值(Price Value of a Basis Point)
PVBP的定義是:△價格/1基點。一個基點是1%的百分之一,所以是0.0001,縮寫是bps
(2) Yield Value of a Price Change
基本上就是把PVBP的定義倒過來,△殖利率(bps)/1元
(3) Duration存續期間
先看張圖

就是這個翹翹板/槓桿的概念,存續期間的存在,把債券殖利率每1單位的變動放大或縮小。
但是!存續期間有好幾種,談到存續期間時,要先講清楚是哪種存續期間?基本上可以分成Macaulay Duration& Modified Duration 兩種。
Macaulay Duration 存續期間
這就是一般泛指的存續期間,定義是:△債券價格%/△殖利率%。
也有人把Macaulay Duration當作是投資債券還本的時間,就如小黑之前說的:

其原理留到數學部分再解釋,基本上Macaulay Duration就是一個衡量債券價格波動的方法。
Modified Duration 修正存續期間
定義是:△債券價格%/△殖利率
跟Macaulay Duration比起來,修正存續期間的分母部分不是用%來衡量。因為一般我們都習慣用利率(殖利率)的絕對數字,而不是比率來衡量其變動。舉例來說,利率從1%升到2%,這個漲幅就是100%,好可怕阿!
利率在經濟體系中是一個level的概念,我們要看的是現在利率上升到什麼程度,對經濟帶來什麼影響,而不是去關注它漲了多少(又不是在交易利率衍生性商品)。
所以,修正存續期間用絕對數字來衡量債券的價格波動,相較Macaulay Duration是比較make sense的
複習一下上一篇介紹的債券價格波動特性,其他條件固定的情況下:
到期時間(maturity)越長,修正存續期間越大。
票面利率(coupon rate)越低,修正存續期間越大。
實務上的修正存續期間算法

因為有時去代數學公式算存續期間太麻煩,實務上我們會用上述式子來逼近修正存續期間,經驗證偏差非常非常的小,這種算法稱得上是方便快速又有效!
P0是債券的初始價格、P-是將殖利率向下微調1bps的價格(會上升)、P+是將殖利率向上微調1bps的價格(會下降)。
對於大多數讀者來說,將債券殖利率、價格波動特性、存續期間瞭解至此就已功德圓滿,但如果有像小丑一樣特別愛較真,非得鑽牛角尖不可的朋友,接下來就一起進入數學推導部分吧XD
Macaulay & Modified Duration數學推導
Macaulay Duration= △債券價格%/△殖利率%
要計算變化率的話,數學上就是針對yield去求一階導數
債券價格:
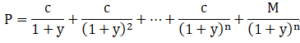
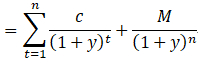
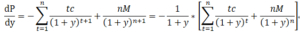
同時拿P針對1+y去求一階導數也是得到相同結果,dp/dy=dp/d(1+y)
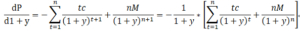
將dp/dy乘以1/P就得到了修正存續期間:
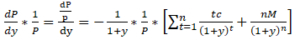

分子的dP/P代表價格的變化率(%),分母的dy則是殖利率的變化量。
將修正存續期間的dy改成d(1+y),再把等號兩邊都乘以1+y,就得到了Macaulay Duration
當初是先求得Macaulay Duration,然後就如上面說的用單純的利率變動基點來衡量比較make sense,所以後來才求得Modified Duration。
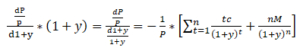
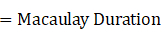
上面提到有人將Macaulay Duration當作債券回本的時間,詳細看公式,會發現這是因為在票面利率的那一項,每個c前面都乘上一個時間t=n, n=1,2,…,n,本金M的前面也乘上一個n,代表說債券的每一期的現金流都被期數加權了(被t=1,2,…,n加權)。所以正常來說,存續期間不會超過到期時間(maturity)。
但事實上這是一個危險的看法,只適用於沒有隱含選擇權的債券。所謂的隱含選擇權就是債券的callable or putable provision,或者MBS這種可以提前攤還本金的權利。也就是說遇到會被call回、可以提前賣回、可以提前攤還本金的證券,修正存續期間可能會超過maturity,所以還是當作衡量價格波動性的指標比較穩妥。
針對有隱含選擇權的固定收益證券,有另外一個衡量價格波動性的存續期間,叫做有效存續期間(Effective Duration),之後再撰文分享。
封面圖片來源:pixabay




