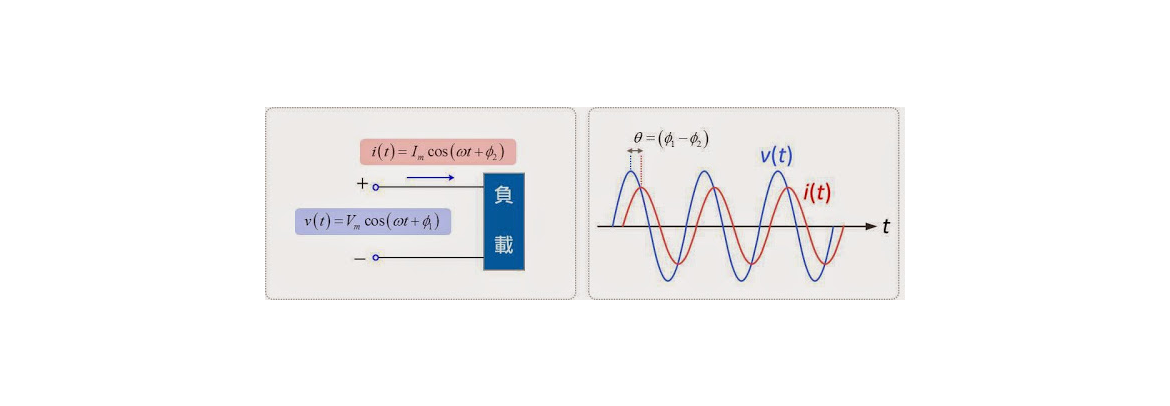
當我們在電路學中學到交流電的時候,一定會學到如何計算交流電的平均功率。(註:這裡的交流電,我指的是比較狹義的正弦波訊號,而非廣義的極性改變的那種交流電)
接下來就是一張圖,這張圖只畫了一個負載,老師告訴你負載上的電壓跟電流的樣子是什麼。當然,「長怎樣」其實已經用數學描述了,但我再奉送一下波形圖,藍色的是電壓波形、紅色的是電流波形。
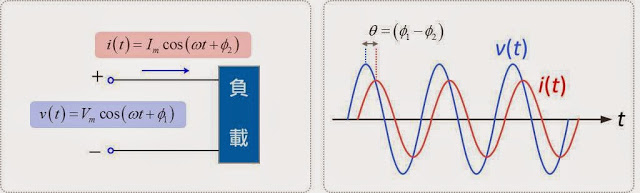
然後,經過一連串推導,就得到了負載所消耗的平均功率 P:
\begin{align} P=\frac{1}{2}V_{m}I_{m}cos\left ( \phi_{1}-\phi_{2} \right )=\frac{1}{2}V_{m}I_{m}cos\left ( \theta \right )=V_{rms}I_{rms}cos\left ( \theta \right )=\left | S \right |cos\left ( \theta \right ) \end{align}
其中的 \begin{align} P. F. = cos\left ( \theta \right ) \end{align}又稱為 Power Factor (P.F., 功率因素),如果負載是純電阻的話,那麼在負載上施以交流電壓,噴到負載的電流則與電壓同相,兩者沒有相差,此時負載拿到的功率就是很純的實功率。如果負載不是純電阻,有一些電抗性存在,那麼負載上的電壓與電流就會有相差,因而 PF 將小於 1。
好啦!停~~~~~ 我沒有要討論這些公式以及實阿、虛阿、張三、李四的意思~
我們看到後面有個 |S|,S 稱之為複數功率(Complex Power),公式如下,粗體 V 跟 I 是正弦電壓跟電流波的相量(Phasor)。
註1:sorry, 此處不討論為什麼 S 就是 V 的相量乘上 I 相量的共軛, 這個大家就自己看書吧~ 我也不討論什麼是 phasor, 更沒有要討論 phasor 的物理意義,有時間再說。
註2:以下的相量是使用峰值表示法 (如果你看我的電路學講義第7章第35頁, 少了1/2, 講義裡頭是使用rms表示法)
\begin{align*} S=\frac{1}{2}\mathbf{VI}^{*} \\
P=\frac{1}{2}Re\left \{ \mathbf{VI}^{*} \right \} \\
Q=\frac{1}{2}Im\left \{ \mathbf{VI}^{*} \right \} \end{align*}
複數功率 S 的單位是 VA (電壓乘電流嘛~)
它的實部 P 稱為實功率或有效功率,單位為 Watt (其實也是 VA,但說 W 或 Watt 大家就知道是在講實功率)
它的虛部 Q 稱為虛功率或無效功率,單位為 VAR (R是Reactance, 電抗的意思)
複數功率 S 的絕對值 |S| 稱為視在功率(apparent power),英文的apparent就是顯而易見的意思。問題來了,為什麼 |S| 就是那麼顯而易見?為什麼一看就知道它在哪兒!為什麼 S 就不那麼"視在",|S| 比起來就比較視在?難道S加個絕對值就變的比較屌?
是啊!是很屌~ (我掰不下去了⋯⋯,因為我也不知道屌在哪~)
讓我們把時間拉回舊石器時代,當時的科技並不發達,人類首次懂得使用鑽木取火... (喂~~~)
好啦!就是工程師手邊只有鳥鳥的三用電表,要嘛就跟負載並聯量一下電壓,要嘛就跟負載串聯量一下電流⋯⋯,就算有兩台三用電表同時使用,量出來的電壓、電流都是數字,哪能知道 V 跟 I 之間有什麼相差啊!是不是!所以,工程師只看得出 V 跟 I 的值,但不知道兩者間的相對關係。
如果電表量出來的電壓是峰值 Vm、電流是峰值 Im,又或者是RMS值也可以。工程師就會說:哦!Apparently,這個功率就是
\begin{align} P_{apparent}=\frac{1}{2}V_{m}I_{m}=\left | S \right | \end{align} 或
\begin{align} P_{apparent}=V_{rms}I_{rms} =\left | S \right | \end{align}
關於這件事情的真實性,就由這位小弟弟來回答吧!我的唬爛到此為止⋯⋯哈哈哈哈!
YOTTA 你最專業的學習夥伴,提供優質內容與有趣觀點,擴大豐富你的視野。
- 訂閱李健榮 Simen的專欄,看更多文章。
- 一起學習「EE心法|相量之道」。